Typical Measures for Force Generation and Stresses in Cells¶
There is a number of different ways to measure force generation and stresses. Here you can find an overview of all quantities that can be calculated with this program.
Deformations in the Substrate¶
The simplest way is to sum up all deformations on the substrate surface that the cells are attached to. The deformations depend on the mechanical properties of the substrate, which means that this is not possible to compare results, when different substrates have been used.
Strain Energy¶
The strain energy is the total work that cells have to commit to deform their substrate. It is defined as \(\frac{1}{2} \int \vec{d} \times \vec{f}\), where \(\vec{d}\) and \(\vec{f}\) are the deformation and the traction force vectors. That means that a high strain energy only needs a local alignment of both vectors.
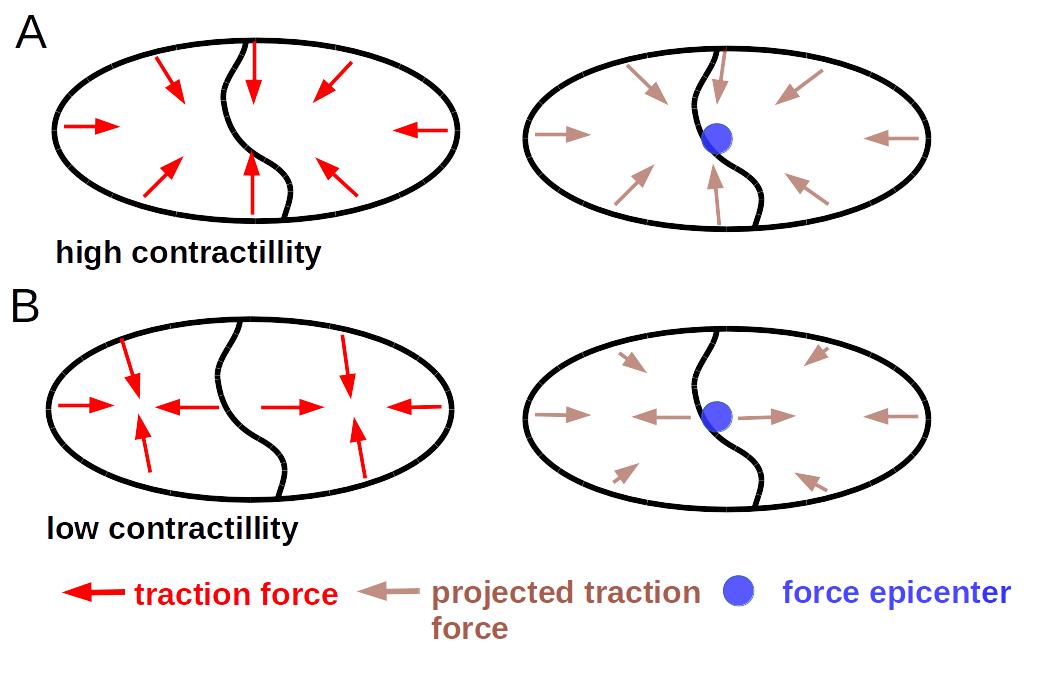
Contractility¶
The contractility is defined as the sum of the projection of all traction forces towards one point, called the force epicenter. As such, the contractility is high if all force are already orientated towards one central point. Locally opposing forces and forces not pointing towards the force epicenter do not contribute to the contractility. A cell or cell colony which is able to coordinate its force generation in such a way that the forces seem to originate from a single point can achieve a high contractility, while expending a comparably small amount of strain energy.
This is further illustrated in Fig. 13. Case A represents a cell colony with two cells with high coordination of force generation and Case B represents a cell with coordination. In case B each cell generates contractile forces on its own. Accordingly case B has a lower contractility if we assume equal strain energy in Case A and B.
To sum up: the strain energy is a measure for the total force generation, while the contractility is a measure for the coordinated force generation.
Average Normal and Shear Stress¶
Stress describes the forces that are transferred inside of a cell or cell sheet. For any given point in the cell sheet the stress is defined by a tensor with 4 components. Each component represents forces that would act on the edges of a square that was cut out of the cell sheet as shown in Fig. 14.
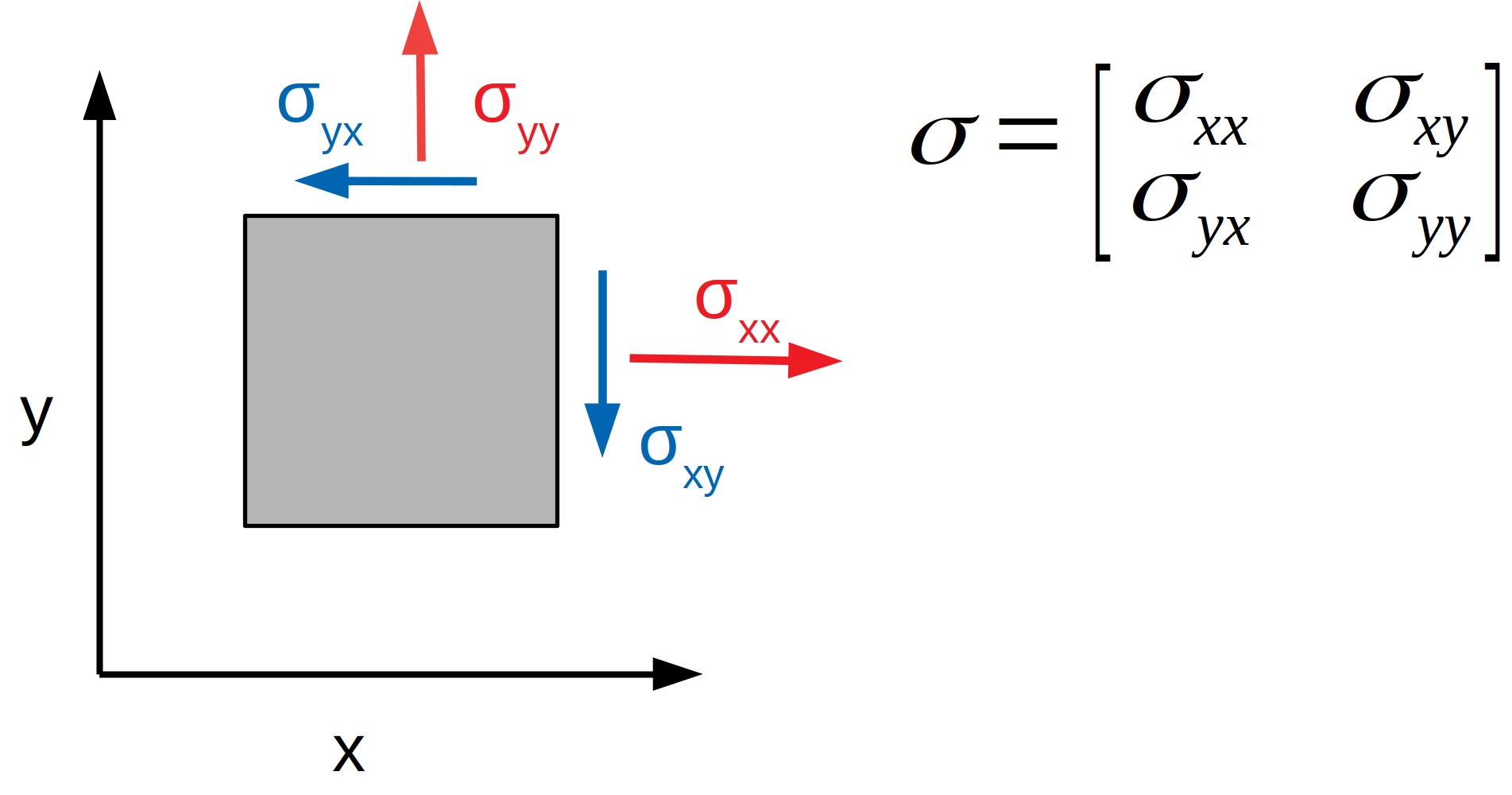
Fig. 14 \(\sigma_{xx}\) and \(\sigma_{yy}\): Normal Stresses in x and y direction. \(\sigma_{xy}\) and \(\sigma_{yx}\): Shear stresses.
We can distinguish between two types of stress: The shear stress, a force that acts parallel to the edges of this square, and normal stress, a forces that acts perpendicular to the edges of this square. Due to geometric reasons both shear components of the stress tensor must be identical. This is not the case for the normal components. Since it is of no interest whether normal stress comes predominately from the x or y directions for our analysis, it is more useful to calculate the mean of both components. This leaves two stresses: the shear stress and the mean normal stress. These stresses can be averaged over the whole cell colony area.
Note
The mean normal stress can be either negative, indicating a compressive stress, or positive, indicating a tensile stress. A typical cell experiences tensile stress, as it pulls on the underlying substrate from its edges .The shear stress can also have a positive or a negative sign. However, there is no useful interpretation in this case.
Distribution of Stresses¶
The distribution of stresses can be described by the Coefficient of Variation (CV), that is the standard deviation normalized with the mean, of mean normal or shear stress.
Forces acting across Cell Boundaries¶
As hinted above, the stress tensor can be used to calculate the force that acts across a boundary in the cell colony. This force is called the line tension, and has a straight forward interpretation: Imagine you were to actually cut the cell sheet along the boundary between two cells. If the cells continue to generate force the edges of this cut would drift apart or start overlapping as you have just cut the material holding both edges together. In order to hold both edges in place as they were before you cut them, you need to apply a force at the edges. This force, normalized by the length of the cut, is the line tension.
The line tension is a vector with x and y components. Similar to stresses it can be split in a shear component (the force acting parallel to the cut) and a normal component (the force acting perpendicular to the cut). Both contribute to the magnitude (length of the line tension vector) of the line tension.
Note
Similar to normal stresses, the normal component of the line tension can be negative or positive, indicating that the two sides of the edge along which the line tension was calculated, are pushed together or pulled apart. The shear component of the line tension lacks such an interpretation and the magnitude of the line tension can of course only be positive.